Devoir en commun de maths en cinquième (5ème) - Mathématiques - Classe de Cinquième (5ème)
Un devoir en commun de maths en cinquième (5ème) est toujours un moyen pour les élèves de s’expliquer entre eux et de combler certaines lacunes en maths. Ce devoir en commun de maths vous aidera à développer des compétences.
Devoir commun de mathématiques 5e
Exercice 1 :
Calculer les expressions mathématiques A, B et C en détaillant les calculs.
A = 10 – 4 + 2 B = 15 + 2 × 5 C = 10 × [ 5 + 4 ÷ (10−8) ]
Exercice 2 : ‘devoir en commun de maths’
Cet exercice est un questionnaire à choix multiple (Q.C.M).
Aucune justification n’est demandée.
Pour chacune des questions, trois réponses sont proposées. Une seule est exacte.
Pour chacune des questions, indiquer sur la copie le numéro de la question et recopier la réponse exacte.
| Réponse A | Réponse B | Réponse C | Réponse D | ||
|
N°1 |
J’ai un rectangle ABCD avec AB = 12 cm et BC = 6cm. Quel est son périmètre? |
36 cm |
36 cm² |
72 cm² |
72 cm |
|
N°2 |
AB = 8,4 cm
AC = 3,4 cm BC = 7 cm |
Le point C appartient au segment [AB] |
La figure est impossible |
Le triangle ABC est constructible |
Le point A appartient au segment [BC] |
|
N°3 |
Un grand magasin reçoit sa livraison de jus de fruit, soit 18 cartons de 12 bouteilles. Il reste en réserve 102
bouteilles. Combien y a-t-il maintenant de bouteilles de jus de fruit dans ce grand magasin ? |
(12+102)x18 |
(18+102)÷12 |
102+12×18 |
(18+102)x12 |
|
N° 4 |
Quelle est la droite qui passe par un sommet
et qui est perpendiculaire au côté opposé ? |
La parallèle |
La médiane |
La médiatrice |
La hauteur |
Exercice 3 :
Ranger les nombres suivants dans l’ordre croissant :
Exercice 4 : ‘devoir en commun de maths’
1. Placer sur une droite graduée d’origine O les points A, B et C d’abscisses respectives -4 ; -2 ; + 3.
2. Léo observe la droite et dit :
« Avec une autre origine O’, les points ont pour abscisses : A(-1) ; B (+ 1) ; C(+ 6) ».
Placer en bleu sur la droite graduée ce point O’
Exercice 5 :
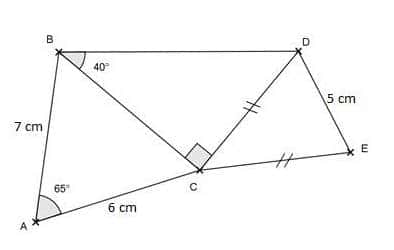
La figure ci-dessous a été tracée à l’aide du logiciel geogebra.
Sur la copie, construire en vraie grandeur cette figure, l’unité de longueur étant le centimètre.
(Laisser les traits de construction apparents).
Exercice 6 : ‘devoir en commun de maths’
On sait que :
- E est le milieu de [CB]
- CD = 3 cm
- AB = 6 cm
- (CD) est perpendiculaire à (AB)
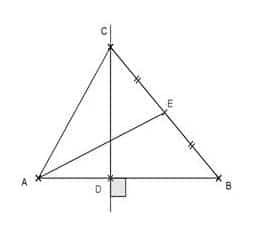
1. Calculer l’aire de ABC
2. Calculer l’aire du triangle CAE. Justifier le calcul.
Exercice 7 :
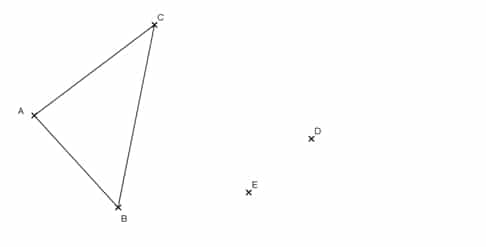
1. Construire, ci-dessous, le point E’ symétrique du point E par rapport à D.
2. Construire, ci-dessous, le triangle A’B’C’ symétrique de ABC par rapport à D.
Laisser les traits de construction apparents.
3. Démontrer que les droites (AB) et (A’B’) sont parallèles.
Outils:
Mathématiques - Évaluation maths 5ème PDF
Devoir en commun de maths en 5ème à télécharger en PDF - Mathématiques Devoir en commun de maths en 5ème à télécharger en PDF
Contrôle sur le calcul littéral en maths en 5ème à télécharger en PDF - Mathématiques Contrôle sur le calcul littéral en maths en 5ème à télécharger en PDF
Devoir en commun de maths en cinquième (5ème) - Mathématiques Devoir en commun de maths en cinquième (5ème)
L’ARBRE DU KIWI EST APPELÉ L’ACTINIDIA